“- А почему я должен следовать правилу? – может возмутиться кто-то. – Я не хочу!”

Что ж, давайте рассмотрим такие примеры.

Древняя Греция. Необходимо доставить из каменоломен колонны для храма Парфенон. Колонны большие – проломят любую повозку. Греки нашли выход: взяли и покатили заготовки колонн по дороге…

Прошли века. Летом 1834 года для Смольного собора в Петербурге понадобилось доставить из города Валдая 12 колоколов, самый крупный из них весил 10 тонн. Как доставить по бездорожью такой груз? Долго мучались, наконец догадались – колокол положили на бок, обшили досками и… покатили, используя силу 15 лошадей.

Уже в начале XX века возникла схожая задача: как перевозить стволы корабельных орудий? Русский инженер В.Г. Шухов надел на них колеса и… А дальше мы уже знаем.

О чем это говорит?

Если, решая задачу, найден сильный “ход” – разумно запомнить его и использовать еще раз при решении схожей. А если не переносить принцип решения с задачи на задачу? Обычно это ведет к напрасной трате сил, нервов, денег.

Так, лишь несколько лет назад догадались: чтобы перемесить снизу насыпи новый рельс на замену старого, не обязательно вызывать мотовоз с краном или, выбиваясь из сил, двигать рельс ломами – на него надо надеть колеса и катить…

В ТРИЗ этот прием получил свое название – принцип сфероидальности.
 

Суть принципа сфероидальности: Если предмет трудно перемещать – дострой его до круглой и легкоперекатываемой формы…

В 1946 году, рассуждая подобным образом, 20-летний бакинский изобретатель Генрих Саулович Альтшуллер приступил к созданию ТРИЗ – теории решения изобретательских задач.

На чем она основана?

Не на случайных “озарениях” чудаковатого изобретателя, которого так любят изображать в кино. Нет. ТРИЗ основана на изучении красивых и сильных решений и выведении из них эффективных приемов устранения противоречий (вспомним “принцип копирования”, “принцип сфероидальности”) и других инструментов решения задач.

К настоящему времени выявлено 40 приемов устранения системных (технических) противоречий.

Приведем ответы на задачи, полученные с применением приема принцип копирования.

В задаче 1 об измерении бревен надо измерять не сами бревна, а их оптическую копию. За несколько минут можно сфотографировать бревна с открытой стороны вагона. К бревнам надо приложить линейку – для определения масштаба. И поезд можно отправлять: все измерения будут сделаны по снимкам.

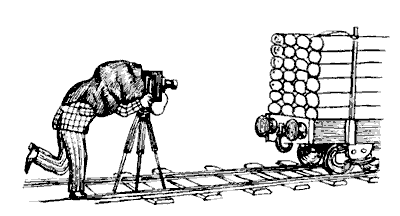Абсолютно то же самое решение годится и для задачи 5 об измерении змеи. Если трудно измерять змею, надо заменить ее на оптическую копию. Сфотографируем змею и будем проводить измерения по фотографии. Надо только сделать так, чтобы рядом со змеей на снимке (для масштаба) присутствовала линейка или какой-либо предмет с точно известными размерами.

В задаче 3 о работающем телевизоре в освещенной комнате вряд ли будут удачными такие решения, как перегородить комнату ширмой, сделать козырек от света над экраном и т.п. А вот изобретательское решение: если трудно использовать ширму, возьмем ее миниатюрную копию - на бок лампочки, обращенной к телевизору, наклеивается кусочек непрозрачного материала, скажем, фольги. Теперь в одной комнате и лампочка горит, и телевизор работает – и друг другу не мешают. Ведь тень от фольги как раз приходится на экран… Красиво?!

Для задачи 4 о тренировках в паре с чемпионом ответ таков: график движения чемпиона легко задается “копией”, например, движением луча света по беговой дорожке.

Copyright © 2000 ТРИЗ-группа (Великий Новгород)